公司内部系统/平台(最常见、最官方)
这是最直接、最权威的渠道,大多数公司会将制度文件发布在内部平台上。

-
内部知识库/文档中心
- 名称可能包括:Confluence、SharePoint、公司内网、知识库、文档中心等。
- 如何查找:
- 在搜索框中直接输入关键词,如“奖励制度”、“激励办法”、“绩效奖金”、“年终奖”、“项目奖”、“销售提成”等。
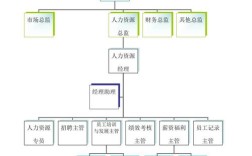
- 浏览组织架构或人力资源相关的板块,通常会有“人力资源部”、“员工发展”、“薪酬福利”等栏目。
- 查看公司发布的年度或季度性通知,HR部门通常会附上相关制度的链接。
-
人力资源信息系统
- 名称可能包括:HR Portal、HR Self-Service、员工自助服务平台等。
- 如何查找:
- 登录系统后,在“薪酬福利”、“绩效管理”或“我的信息”等模块中,通常会有详细的薪酬构成、绩效评估标准和奖金计算规则的说明。
-
内部通讯/邮件系统
- 如何查找:
- 搜索邮件:在公司的邮件系统(如 Outlook, 企业微信)中,用关键词“奖励制度”、“通知”、“邮件主题:..的奖励办法”进行搜索。
- 关注公告:留意来自人力资源部或公司高层的全员邮件,新制度的发布通常会通过邮件通知。
- 如何查找:
咨询相关部门(最有效、最直接)
如果在网上找不到,直接咨询相关人员是最快的方法。

-
直接询问你的直属上级
- 为什么:你的上级最清楚与你绩效直接挂钩的奖励规则,比如项目奖金、绩效奖金等,他们可以为你解释具体的评估标准和发放流程。
-
联系人力资源部
- 为什么:HR部门是公司所有薪酬福利和激励政策的制定者和解释者,他们是获取最权威信息的最终来源。
- 如何联系:
- 发送邮件给HR部门或你所在区域的HR Business Partner(HRBP)。
- 通过内部通讯工具(如企业微信、钉钉)联系HR。
- 电话联系HR的咨询热线。
- 可以问:“您好,我想了解一下公司最新的奖励制度在哪里可以查看?我想了解关于[具体奖励类型,如年终奖/项目奖]的具体条款。”
-
询问入职导师或老员工
- 为什么:对于一些不成文但实际存在的“潜规则”或传统奖励方式,老员工往往更了解,他们可以为你提供制度之外的实用信息。
公司文件/物理公告
一些规模较小或数字化转型较慢的公司,可能会使用传统方式。

-
员工手册
新员工入职时通常会收到一本员工手册,里面会包含薪酬福利、奖惩制度等核心内容,可以找一本电子版或纸质版来查阅。
-
公司公告栏
在茶水间、休息区或办公区域的公告栏,有时会张贴重要的制度通知或文件。
总结与建议
| 途径 | 优点 | 缺点 | 适合情况 |
|---|---|---|---|
| 内部系统/平台 | 官方、权威、信息全面 | 需要花时间搜索,可能找不到 | 大多数公司,特别是有完善内部系统的公司 |
| 咨询相关部门 | 快速、直接、可互动 | 依赖他人的响应时间 | 紧急问题,或在网上无法找到答案时 |
| 公司文件/公告 | 传统、直观 | 信息可能过时,查找不便 | 小型公司或传统行业 |
给您的最佳操作建议:
- 首选“内部系统/平台”:先花几分钟时间在公司内网或知识库里搜索,这是最规范的做法。
- 次选“咨询直属上级/HR”:如果找不到,不要犹豫,直接去问,问HR最权威,问上级最实用。
- 保持积极态度:询问奖励制度表明你对公司有归属感,并希望做出更大贡献,这是一个积极的行为,领导和HR通常会很乐意解答。
希望这些信息能帮助您快速找到公司内部的奖励制度!